Deutschland – Bruttosozialprodukt seit 1950
Das typische Problem „älterer Volkswirtschaften“ wie z.B. der BRD bedingt durch den Zinseszins verdeutlicht die Grafik, die den exponentiellen Verlauf des Zinseszinses und die typische Wachstumskurve einer Volkswirtschaft gegenüberstellt. Anhand der Wachstumsraten „älterer Volkswirtschaften“ kann man ablesen wie die Wachstumsraten, bedingt durch den immer höheren nominalen Ausgangswert immer geringer werden und die Anzahl der Rezessionen zunimmt.
In der derzeitigen Wirtschaftskrise fordern Politik, Gewerkschaften und Wirtschaft in der Presse umgehende und umfassende Maßnahmen, das Wirtschaftswachstum wieder auf einen deutlichen Wachstumskurs zu bringen ungeachtet der Tatsache, dass in einer „alten Volkswirtschaft“ das Bruttosozialprodukt sich jedes Jahr – so es denn im Vorjahr ein Wachstum gab – auf einen immer größeren Ausgangsbetrag bezieht. In „alten Volkswirtschaften“ wie z.B. den europäischen Volkswirtschaften bedeutet ein 2-prozentiges Wachstum je nach Land und durchschnittlicher Wachstumsrate der jeweiligen Volkswirtschaft in den letzten sechzig Jahren mengenmäßig viermal oder fünfmal so viel Wachstum wie in den fünfziger Jahren.
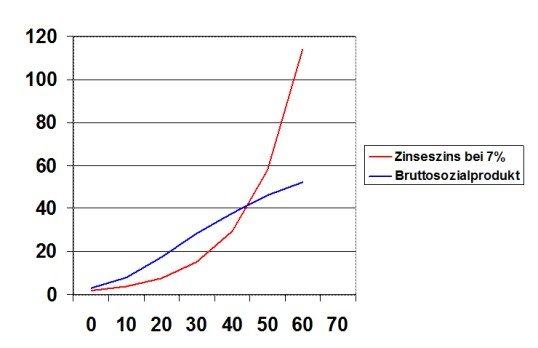
Beispiele für den exponentiellen Verlauf einer Volkswirtschaft über Jahrzehnte
Nachteile durch Zinses Zins
Wie hat sich der Zinseszins bei der Wirtschaftskrise verändert? Unter dem Zinses Zins versteht man eine Brechung der Zinsen, auf ein Kapital oder auf seine bereits beglichen Zinsen. Durch die Krise sind die Zinseszinsen angestiegen, sodass man hier mehr bezahlen muss, wenn man seine Zinsen, für das Leihen von Geld oder etwas Anderem, zurückbezahlen möchte. Dies ist mittlerweile soweit, dass nur ein kleiner Teil (10 Prozent) der deutschen Bevölkerung von den Zinsen profitieren kann. Weitere 10 Prozent halten sich mit den Zinsen und den Ausgaben die Wage und die letzten 80 Prozent, zahlen bei ihren Zinsen fast täglich drauf, sodass es sich für diese nicht lohnt.
Mit den Vorteilen von Zinsen die man auf sein Guthaben bekommt, kann man durchaus einen hohen Gewinn machen, andererseits bringt der Zinseszins (spätestens seit der Welt Wirtschaftskrise) einige große finanzielle Nachteile mit sich, die man berücksichtigen sollte, um hier keinen Verlust zu machen.
Anschauliche Beispiele für das exponentielle Wachstum des Zinseszins
Im Folgenden sollen einige Beispiele das Phänomen des exponentiellen Wachstums anschaulich erklären. Exponentielles Wachstum wird von den wenigsten Menschen verstanden, weil es in unseren natürlichen Lebensprozessen (fast) nicht vorkommt. Ein weiteres Merkmal dieser Art des Wachstums besteht darin, dass die Kurven plötzlich immer steiler werden und damit ein Überraschungseffekt eintritt. Exponentielles Wachstum liegt vor, wenn eine Basismenge prozentual wächst. Es kann zur Katastrophe führen, wenn es nicht in einem frühen Stadium begrenzt wird.
Beispiel 1
In einer mittelgroßen Stadt (60.000 Einwohner) wurde die Bevölkerung gefragt, welches Wachstum sie für angemessen hielte. Die meisten fanden 10% Bevölkerungszuwachs pro Jahr nicht übertrieben.
Das bedeutet aber folgende Entwicklung:
nach einem Jahr: 66.000
nach 2 Jahren: 72.600
nach 3 Jahren: 79.600
nach 4 Jahren: 87.846
nach 5 Jahren: 96.630
nach 6 Jahren: 106.294
nach 7 Jahren: 116.923, also fast eine Verdopplung!
Damit hatte keiner gerechnet. Wenn dieses Wachstum so weiter geht, hat die Stadt nach weiteren 20 Jahren 1 Million Einwohner! So lässt sich auch die rasante Entwicklung der Weltbevölkerung erklären.
Beispiel 2
In einer Ecke eines Teiches beginnen Seerosen so zu wachsen, deren Fläche sich täglich verdoppelt. Zunächst fällt die bedeckte Fläche nicht so auf – nach 27 Tagen ist erst ein Achtel der Seefläche bedeckt. Frage: Wie viele Tage dauert es, bis der ganze See bedeckt ist? Antwort nur 3 Tage! Am 28. Tag ist ein Viertel bedeckt am 29. Tag die Hälfte und am 30. Tag ist der See vollständig zugewachsen.
Beispiel 3
Dem Erfinder des Schachspiels wurde von einem dankbaren Herrscher in China die Erfüllung eines Wunschs zugesichert. Der Erfinder erbat sich pro Tag eine Menge Reis, die sich durch folgende Prozedur ergibt: Auf das erste Schachfeld wird am ersten Tag ein Reiskorn gelegt, auf das zweite am zweiten Tag die doppelte Menge, also 2, auf das dritte wiederum die doppelte Menge, also 4, und so weiter bis zum 64. Feld am 64. Tag. Dem Herrscher schien die Bitte leicht erfüllbar –als aber am Ende des ersten Monats die Reismenge für diesen Tag auf 35 Tonnen angewachsen war, musste er einsehen, dass bei Erfüllung des Wunsches alle Reisernten dieser Welt nicht ausreichen würden!
Beispiel 4
Ebenso wie bei der Reiskornlegende verhält sich ein dünnes Blatt Papier wenn es mehrmals gefaltet wird. Dieses wird immer dicker (und kann in der Regel maximal 10 Mal gefaltet werden). Auch hier liefert die Tatsache, dass sich die Dicke des Papiers immer bezüglich des neuen Ausgangswertes verdoppelt, ein verblüffendes Ergebnis.
Beispiel 5
Das Wachstumsverhalten von Krebszellen beim Befall eines Organismus entspricht ebenfalls exponentiellem Wachstum. Anfangs entwickelt sich der Krebs nur langsam, dann nimmt sein Wachstum, schnell zu. Aus einer Zelle werden 2, aus 2 werden 4, daraus 8, 16, 32, 64, 128, 256, 512 usw. Der Krebs kennt keine natürliche Grenze und wächst unaufhaltsam weiter. Wenn er von Ärzten entdeckt wird, hat er meist schon ein fortgeschrittenes Stadium erreicht und es wird schwer ihn zu heilen. Ein derartiges exponentielles Wachstum in der Natur findet meist dort statt, wo Krankheit oder gar Tod die Folge sind. Der Krebs wuchert im menschlichen Körper und schwächt ihn dabei, bis dieser nicht mehr weiter belastbar ist. Letztlich geht aber mit dem befallenen Organismus auch der Krebs selbst zugrunde. (Daher spricht man hier auch vom begrenzten exponentiellen Wachstum).